7 hằng đẳng thức lớp 8
Cơ Sở Của Đại Số
Hằng đẳng thức cung cấp nền tảng cho các khái niệm trong đại số. Chúng giúp học sinh hiểu rõ hơn về mối quan hệ giữa các biểu thức đại số và cách chúng có thể được biến đổi.
Giúp Giải Quyết Bài Toán Nhanh Chóng
Sử dụng hằng đẳng thức cho phép học sinh giải các bài toán một cách nhanh chóng và hiệu quả hơn. Thay vì thực hiện các phép toán phức tạp, học sinh có thể áp dụng trực tiếp các hằng đẳng thức để tìm ra kết quả.
Phát Triển Tư Duy Logic
Việc học và áp dụng hằng đẳng thức giúp học sinh rèn luyện tư duy logic và khả năng phân tích. Họ phải xác định đúng loại hằng đẳng thức nào cần sử dụng trong mỗi tình huống cụ thể.
Ứng Dụng Trong Giải Hệ Phương Trình
Hằng đẳng thức là công cụ hữu ích trong việc giải hệ phương trình và bất phương trình. Chúng giúp đơn giản hóa các biểu thức phức tạp và tìm ra nghiệm của phương trình dễ dàng hơn.
Liên Kết Với Các Khái Niệm Khác
Hằng đẳng thức không chỉ tồn tại trong đại số mà còn liên kết với hình học, như trong việc tính diện tích và thể tích. Sự liên kết này giúp học sinh thấy được sự thống nhất của toán học.
Chuẩn Bị Cho Các Bài Học Cao Hơn
Việc nắm vững hằng đẳng thức ở lớp 8 sẽ giúp học sinh chuẩn bị tốt hơn cho các kiến thức toán học nâng cao hơn trong các lớp tiếp theo, như đại số cao cấp và giải tích.
Khuyến Khích Tính Sáng Tạo
Học sinh có thể sáng tạo trong việc áp dụng hằng đẳng thức để giải quyết các bài toán khác nhau. Điều này không chỉ giúp họ hiểu rõ hơn về kiến thức mà còn phát triển khả năng tư duy sáng tạo.
Hằng đẳng thứcLịch Sử Phát Triển Đại Số
Đại số đã có từ hàng ngàn năm trước, với các nhà toán học như Al-Khwarizmi (thế kỷ 9) đóng vai trò quan trọng trong việc phát triển các khái niệm đại số. Các hằng đẳng thức đã được hình thành từ những nghiên cứu về các biểu thức đại số và các phép toán liên quan.
Cơ Sở Hình Học
Nhiều hằng đẳng thức có nguồn gốc từ các khái niệm hình học. Ví dụ, hằng đẳng thức (a + b)² = a² + 2ab + b² có thể được chứng minh thông qua việc tính diện tích của hình vuông bao quanh cạnh (a + b).
Phát Triển Từ Các Nhà Toán Học Cổ Điển
Các nhà toán học cổ điển như Euclid và Pythagoras đã nghiên cứu các mối quan hệ giữa các đại lượng, dẫn đến sự hình thành các hằng đẳng thức. Họ đã sử dụng các phương pháp hình học để chứng minh và phát triển các công thức.

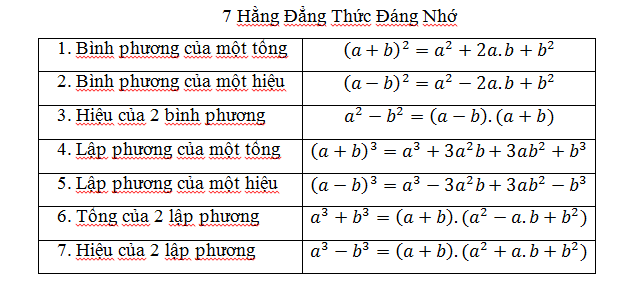
Hằng đẳng thứcHằng Đẳng Thức 1 : (a + b)² = a² + 2ab + b²
Giải thích: Khi bình phương tổng của hai số, kết quả bằng bình phương của từng số cộng với hai lần tích của chúng.
Hằng Đẳng Thức 2 : (a - b)² = a² - 2ab + b²
Giải thích: Khi bình phương hiệu của hai số, kết quả bằng bình phương của từng số trừ đi hai lần tích của chúng.
Hằng Đẳng Thức 3 : a² - b² = (a-b).(a+b)
Giải thích: Hiệu của hai bình phương có thể được phân tích thành tích của tổng và hiệu của hai số.
Hằng Đẳng Thức 4 : a³ + b³ = (a + b)(a² - ab + b²)
Giải thích: Tổng của hai lập phương có thể được phân tích thành tích của tổng và một biểu thức bậc hai.
Hằng Đẳng Thức 5 : a³ - b³ = (a - b)(a² + ab + b²)
Giải thích: Hiệu của hai lập phương có thể được phân tích thành tích của hiệu và một biểu thức bậc hai.
Hằng Đẳng Thức 6 : (a + b)³ = a³ + 3a²b + 3ab² + b³
Giải thích: Khi lập phương tổng của hai số, kết quả bằng tổng của các bình phương và các tích của chúng với hệ số tương ứng.
Hằng Đẳng Thức 7 : (a - b)³ = a³ - 3a²b + 3ab² - b³
Giải thích: Khi lập phương hiệu của hai số, kết quả bằng bình phương của từng số với các hệ số tương ứng.

Hằng đẳng thứcSử dụng câu chuyện hoặc hình ảnh
Hình ảnh: Tưởng tượng một hình vuông cho hằng đẳng thức bình phương. Ví dụ, (a + b)² ,có thể hình dung là một hình vuông lớn được chia thành 4 phần: a²,b² và 2 phần ab.
Câu chuyện: Kể một câu chuyện về hai người (a và b) cùng nhau xây dựng một ngôi nhà (bình phương), trong đó mỗi người đóng góp phần của mình (các phần của hằng đẳng thức).
Sử dụng từ khóa
Bình phương: "Tổng bình phương" và "Hiệu bình phương" dễ nhớ với từ "bình".
Lập phương: Ghi nhớ "Tổng lập phương" và "Hiệu lập phương" với từ "lập".
Thực hành thường xuyên
Giải bài tập: Thực hành giải các bài tập liên quan đến hằng đẳng thức. Càng làm nhiều, bạn sẽ càng quen thuộc với chúng.
Tạo flashcards: Viết mỗi hằng đẳng thức lên một thẻ và ôn tập thường xuyên.
Giải quyết bài toán đại số
Ứng dụng: Hằng đẳng thức giúp đơn giản hóa các biểu thức phức tạp, từ đó dễ dàng tìm ra giá trị hoặc giải phương trình.
Tính giá trị của biểu thức
Ứng dụng: Sử dụng hằng đẳng thức để tính giá trị của biểu thức mà không cần phải thực hiện phép tính phức tạp.
Chứng minh các đẳng thức
Ứng dụng: Hằng đẳng thức có thể được sử dụng để chứng minh các đẳng thức khác trong toán học.
Giải bài toán hình học
Ứng dụng: Một số hằng đẳng thức có thể được áp dụng trong các bài toán hình học, đặc biệt là liên quan đến diện tích và thể tích.
Phân tích đa thức
Ứng dụng: Hằng đẳng thức giúp phân tích các đa thức thành tích của các yếu tố đơn giản hơn, điều này rất hữu ích trong việc giải phương trình bậc hai.
Giải bài tập trắc nghiệm
Ứng dụng: Trong các bài thi trắc nghiệm, hằng đẳng thức có thể giúp bạn nhanh chóng tìm ra đáp án đúng mà không cần phải tính toán quá nhiều.
Trên đây là một số thông tin về 7 hằng đẳng thức lớp 8 bao gồm: tầm quan trọng, nguồn gốc, danh sách các hằng đẳng thức, các mẹo để nhớ 7 hằng đẳng thức đơn giản và ứng dụng của hằng đẳng thức trong các kì thi.