Thể tích khối lập phương
Khối lập phương là một hình khối đặc biệt trong hình học, được tạo thành từ sáu mặt đều là hình vuông. Các cạnh của khối lập phương có độ dài bằng nhau và các góc đều là góc vuông.
Đặc điểm của khối lập phương
6 mặt: Tất cả các mặt đều là hình vuông và có diện tích bằng nhau.
12 cạnh: Tất cả các cạnh đều có độ dài bằng nhau.
8 đỉnh: Tại mỗi đỉnh, ba cạnh gặp nhau tạo thành góc vuông.
Đối xứng: Khối lập phương có tính đối xứng cao, có thể chia thành hai phần bằng nhau theo nhiều cách khác nhau.

Khối lập phươngKý hiệu
a: Độ dài một cạnh của khối lập phương
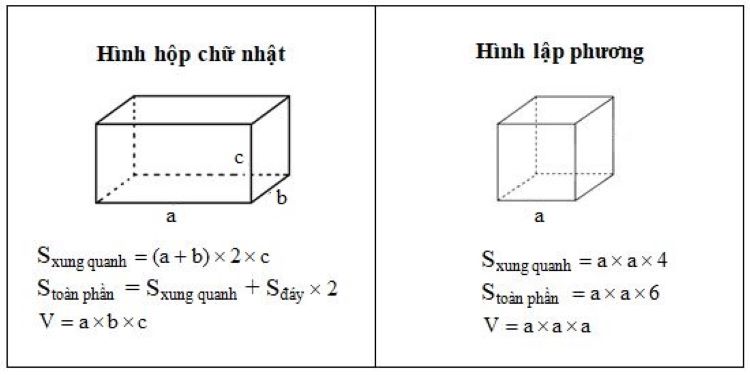
Các công thức
Diện tích:
Diện tích một mặt: S = a²
Diện tích xung quanh: Sxq = 4S = 4a² (Tổng diện tích của 4 mặt bên)
Diện tích toàn phần: Stp = 6S = 6a² (Tổng diện tích của cả 6 mặt)
Thể tích:
Thể tích: V = a³
Đường chéo:
Đường chéo của một mặt: d = a√2
Đường chéo của khối lập phương: d = a√3
Ví dụ
Giả sử bạn có một khối lập phương có cạnh dài 5cm.
Diện tích một mặt: S = 5² = 25 cm²
Diện tích xung quanh: Sxq = 4 * 25 = 100 cm²
Diện tích toàn phần: Stp = 6 * 25 = 150 cm²
Thể tích: V = 5³ = 125 cm³
Khối lập phươngVí dụ 1: Bài toán thực tế
Đề bài: Một bể cá hình hộp chữ nhật có đáy là hình vuông cạnh 50cm, chiều cao của bể là 60cm. Người ta đổ đầy nước vào bể. Hỏi trong bể có bao nhiêu lít nước? (Biết 1dm³ = 1 lít)
Phân tích:
Bể cá có đáy là hình vuông nên chiều dài và chiều rộng của đáy bằng nhau và bằng 50cm.
Thể tích của bể cá chính là thể tích của một khối hộp chữ nhật.
Đ tính được thể tích, ta nhân chiều dài, chiều rộng và chiều cao của bể lại với nhau.
Giải:
Đổi 50cm = 5dm, 60cm = 6dm
Thể tích của bể cá là: V = 5 x 5 x 6 = 150 (dm³)
Vì 1dm³ = 1 lít nên trong bể có 150 lít nước.
Đáp số: 150 lít nước.
Ví dụ 2: Bài toán liên quan đến khối lập phương ghép hình
Đề bài: Có 64 khối lập phương nhỏ cạnh 1cm. Người ta xếp các khối lập phương này thành một khối lập phương lớn. Hỏi cạnh của khối lập phương lớn là bao nhiêu cm?
Phân tích:
Ta cần tìm số lượng khối lập phương nhỏ xếp thành một cạnh của khối lập phương lớn.
Vì 64 = 4 x 4 x 4 nên cạnh của khối lập phương lớn sẽ gồm 4 khối lập phương nhỏ xếp cạnh nhau.
Giải:
Cạnh của khối lập phương lớn là: 1 x 4 = 4 (cm)
Đáp số: 4cm.
Ví dụ 3: Bài toán liên quan đến diện tích và thể tích
Đề bài: Một hộp quà hình lập phương có cạnh 15cm. Người ta dán giấy màu xung quanh hộp quà (không dán mặt đáy). Tính diện tích giấy màu cần dùng.
Phân tích:
Diện tích giấy màu cần dùng chính là diện tích xung quanh của khối lập phương.
Giải:
Diện tích một mặt của hộp quà là: 15 x 15 = 225 (cm²)
Diện tích giấy màu cần dùng là: 225 x 4 = 900 (cm²)
Đáp số: 900 cm².
Bài toán 1: Khối lập phương xếp chồng
Đề bài: Có một chồng các khối lập phương xếp chồng lên nhau. Lớp dưới cùng có 8 khối lập phương, lớp thứ hai có 6 khối, lớp thứ ba có 4 khối và cứ tiếp tục như vậy cho đến khi chỉ còn một khối ở lớp trên cùng. Hỏi có bao nhiêu khối lập phương trong chồng đó?
Gợi ý: Đây là bài toán liên quan đến dãy số. Bạn có thể tìm quy luật của số lượng khối lập phương ở mỗi lớp để tính tổng số khối.
Bài toán 2: Khối lập phương cắt đôi
Đề bài: Một khối lập phương bằng gỗ được cắt đôi theo một mặt phẳng đi qua tâm của khối lập phương. Diện tích của mặt cắt là 32cm². Tính thể tích của khối lập phương ban đầu.
Gợi ý: Mặt cắt là một hình vuông. Từ diện tích hình vuông, bạn có thể tính được độ dài cạnh của hình vuông đó, cũng chính là đường chéo của một mặt của khối lập phương.
Bài toán 3: Khối lập phương và hình hộp chữ nhật
Đề bài: Một hình hộp chữ nhật có chiều dài gấp đôi chiều rộng và gấp ba chiều cao. Biết thể tích của hình hộp chữ nhật là 192cm³. Nếu ta xếp các khối lập phương nhỏ cạnh 2cm vào đầy hình hộp chữ nhật thì cần bao nhiêu khối lập phương?
Gợi ý: Đầu tiên, bạn cần tính kích thước của hình hộp chữ nhật. Sau đó, tính thể tích của một khối lập phương nhỏ. Cuối cùng, chia thể tích của hình hộp chữ nhật cho thể tích của một khối lập phương nhỏ.
Khối lập phươngTrong xây dựng và kiến trúc
Tính toán khối lượng vật liệu:
Dùng để tính thể tích gạch, khối bê tông, gỗ, hoặc các vật liệu xây dựng khác cần thiết để hoàn thành công trình.
Ví dụ: Xác định thể tích gạch lát hoặc khối bê tông cần cho một công trình.
Thiết kế không gian:
Xác định thể tích của một căn phòng hoặc khối hộp chứa thiết bị để đảm bảo đủ không gian sử dụng.
Ví dụ: Đo lường không gian bên trong các khối container hoặc nhà kho.
Trong sản xuất và đóng gói
Tính toán dung tích hộp đựng sản phẩm:
Tính thể tích của các hộp chứa sản phẩm để tối ưu hóa việc đóng gói và vận chuyển.
Ví dụ: Đóng gói đồ điện tử, hộp bánh kẹo, sản phẩm gia dụng.
Tối ưu hóa không gian lưu trữ:
Tính toán để sắp xếp hàng hóa trong kho một cách hiệu quả nhất.
Ví dụ: Đặt số lượng hàng tối đa trong một container hình lập phương.
Trong vận tải và logistics
Xác định tải trọng vận chuyển:
Xác định thể tích hàng hóa để sắp xếp trên các phương tiện vận tải như xe tải, tàu biển, container.
Ví dụ: Tính toán khối lượng hàng hóa có thể chất vào khoang chứa của máy bay hoặc tàu biển.
Tính phí vận chuyển:
Các công ty vận chuyển tính phí dựa trên thể tích kiện hàng để tối ưu hóa chi phí và không gian vận chuyển.
Ví dụ: Tính thể tích kiện hàng trước khi vận chuyển để đảm bảo phù hợp với quy định của hãng vận tải.
Trên đây là một số thông tin về thể tích khối lập phương. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.