Bất đẳng thức Côsi: Công thức, chứng minh và ứng dụng
Trong toán học, có những công cụ đặc biệt không chỉ giúp ta giải nhanh một bài toán mà còn mở ra cách tư duy mới. Bất đẳng thức Côsi chính là một trong những công cụ như vậy. Đây là bất đẳng thức quen thuộc với học sinh phổ thông, thường xuất hiện trong nhiều bài tập chứng minh, rút gọn, cũng như trong các đề thi quan trọng.
Khi nghe đến khái niệm “bất đẳng thức”, nhiều bạn có thể cảm thấy khô khan, khó nhớ và khó áp dụng. Nhưng nếu nhìn ở một góc độ khác, bất đẳng thức Cauchy giống như một “chiếc chìa khóa” giúp bạn mở ra lời giải cho những bài toán tưởng chừng rối rắm. Nó đưa ra một sự so sánh chặt chẽ giữa tổng và tích, cho phép bạn xác định ranh giới giá trị mà các biểu thức có thể đạt tới.
Điểm thú vị là, dù nghe có vẻ hàn lâm, bất đẳng thức Cauchy lại có ứng dụng rất rộng rãi. Bạn không chỉ bắt gặp nó trong các bài toán đại số, giải tích, mà còn trong vật lý, kinh tế học và cả trong phân tích dữ liệu. Nắm vững bất đẳng thức này không chỉ giúp bạn giỏi toán hơn mà còn rèn luyện khả năng suy luận, logic và tính kiên nhẫn.
Khái niệm cơ bản
Bất đẳng thức Côsi, hay còn gọi là bất đẳng thức Cauchy-Schwarz, được phát biểu như sau:
(a1² + a2² + ... + an²)(b1² + b2² + ... + bn²) ≥ (a1b1 + a2b2 + ... + anbn)²
Trong trường hợp đặc biệt với 2 số dương a và b, công thức rút gọn thành:
(a + b)/2 ≥ √(ab)
Điều này có nghĩa rằng trung bình cộng của hai số không bao giờ nhỏ hơn trung bình nhân của chúng.
Ý nghĩa thực tiễn
Nếu bạn từng giải toán tối ưu, tìm giá trị lớn nhất hoặc nhỏ nhất, bạn sẽ thấy bất đẳng thức Cauchy xuất hiện rất thường xuyên. Nó cho phép ta biết rằng có những giới hạn “không thể vượt qua”, từ đó định hướng cách giải nhanh chóng và chính xác.

Minh họa công thức bất đẳng thức Cauchy trong toán họcMột dạng thường gặp là:
(a1² + a2² + ... + an²)(b1² + b2² + ... + bn²) ≥ (a1b1 + a2b2 + ... + anbn)²
Đây là công thức phổ quát được áp dụng trong nhiều trường hợp.
Cách chứng minh dễ hiểu nhất
Hãy bắt đầu từ một biểu thức đơn giản: bình phương của một số luôn không âm. Với hai số thực a và b, ta có:
(a - b)² ≥ 0
Khai triển ra được: a² - 2ab + b² ≥ 0
Từ đó suy ra: a² + b² ≥ 2ab
Chia cả hai vế cho 2: (a² + b²)/2 ≥ ab
Nếu viết lại theo cách khác, ta được: (a + b)/2 ≥ √(ab)
Đây chính là một dạng đặc biệt của bất đẳng thức Cauchy.
Chứng minh mở rộng
Đối với n số không âm, ta có dạng tổng quát:
(a1 + a2 + ... + an)/n ≥ (a1a2...an)^(1/n)
Chứng minh tổng quát đòi hỏi nhiều kỹ thuật hơn, nhưng cách hiểu trực quan là: khi phân phối đều giá trị, trung bình cộng luôn bao phủ và không nhỏ hơn trung bình nhân. Điều này phản ánh sự cân bằng tự nhiên trong toán học: càng đồng đều thì giá trị trung bình càng tối ưu.
Điều kiện áp dụng
Bất đẳng thức Côsi chỉ chính xác khi các số là số thực không âm. Nếu một trong các giá trị âm, kết quả có thể không còn đúng. Do vậy, khi làm bài tập, bạn cần đọc kỹ giả thiết và xác định đúng điều kiện để tránh sai sót.
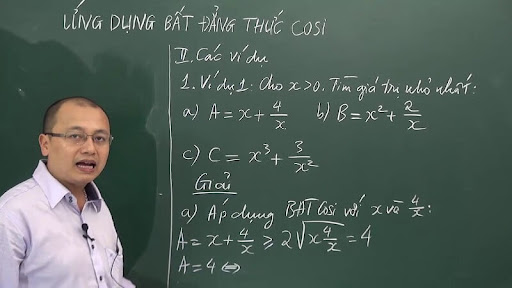
Ví dụ áp dụng bất đẳng thức Cauchy vào bài tập đại sốỨng dụng cơ bản nhất là chứng minh các bất đẳng thức khác. Rất nhiều dạng toán yêu cầu so sánh các biểu thức đều có thể quy về áp dụng bất đẳng thức Cauchy. Ví dụ, khi muốn chứng minh một biểu thức luôn lớn hơn hoặc bằng một giá trị nào đó, bạn có thể biến đổi để xuất hiện dạng của bất đẳng thức.
Trong bài toán tìm cực trị
Một ví dụ đơn giản: tìm giá trị nhỏ nhất của S = (x + y)/2 khi biết xy = 1.
Áp dụng bất đẳng thức Cauchy, ta có: (x + y)/2 ≥ √(xy) = 1
Từ đây kết luận: S ≥ 1. Giá trị nhỏ nhất bằng 1 khi x = y = 1.
Như vậy, thay vì thử nhiều giá trị khác nhau, bạn chỉ cần vận dụng bất đẳng thức để có lời giải gọn gàng.
Trong đề thi và nghiên cứu
Bất đẳng thức Côsi thường xuyên xuất hiện trong đề thi học sinh giỏi, thi đại học. Đặc biệt, nó được kết hợp với các bất đẳng thức khác như AM-GM, Jensen hoặc Holder để tạo nên những bài toán khó, đòi hỏi sự sáng tạo.
Ngoài phạm vi nhà trường, bất đẳng thức Cauchy còn được ứng dụng trong nhiều lĩnh vực nghiên cứu. Chẳng hạn, trong vật lý, nó giúp phân tích các đại lượng dao động; trong kinh tế, nó được dùng để đánh giá hiệu quả phân bổ nguồn lực.
Liên hệ thực tế
Hãy thử nghĩ đến việc chia đều nguồn lực. Nếu bạn có 10 quả táo và muốn chia cho 2 người, cách chia đều (mỗi người 5 quả) sẽ tối ưu hơn rất nhiều so với việc một người nhận 9 quả, người còn lại chỉ có 1 quả. Bất đẳng thức Côsi phản ánh đúng tư tưởng này: sự cân bằng luôn đem lại hiệu quả cao nhất.
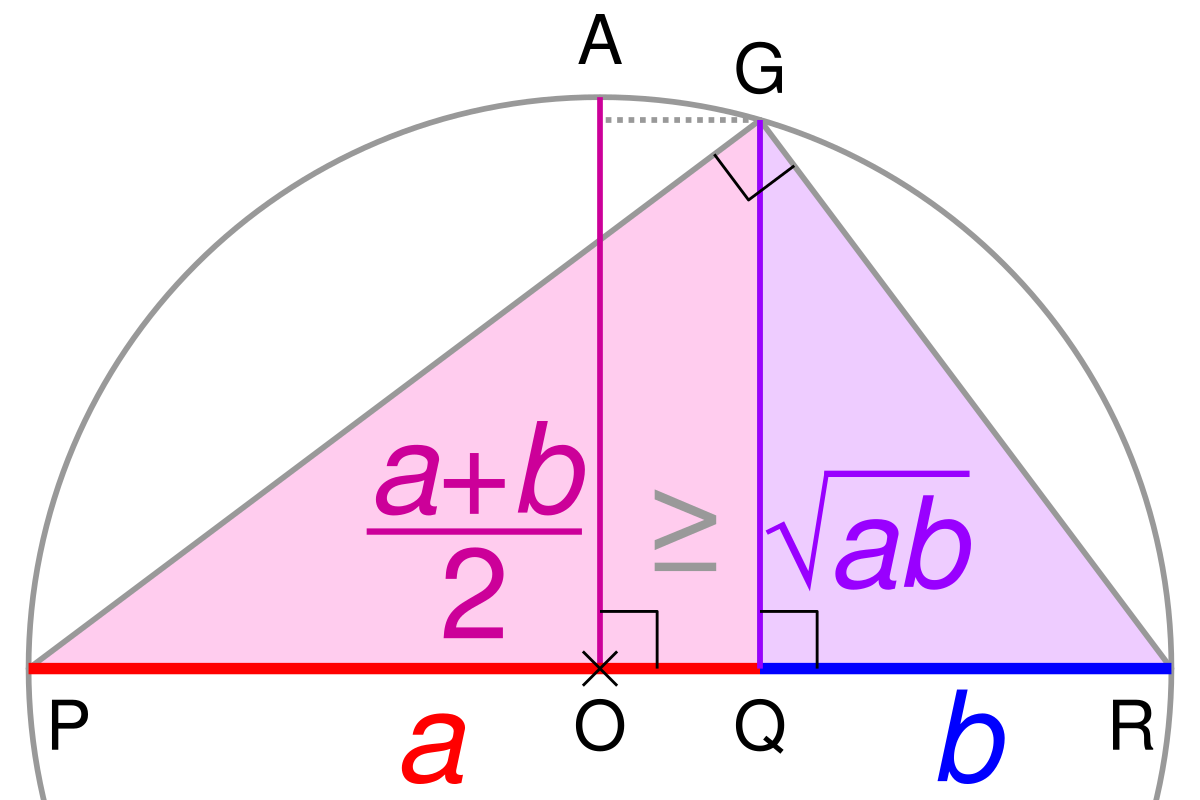
Biểu đồ trực quan hóa bất đẳng thức CauchyĐể học tốt bất đẳng thức Cauchy, bạn không chỉ cần ghi nhớ công thức mà còn phải luyện tập với các ví dụ cụ thể. Dưới đây là một số minh họa giúp bạn hình dung rõ hơn.
Ví dụ 1: Với a, b > 0, chứng minh rằng (a + b)/2 ≥ √(ab).
Lời giải: Xuất phát từ (a - b)² ≥ 0, ta có a² + b² ≥ 2ab. Suy ra (a + b)/2 ≥ √(ab).
Ví dụ 2: Cho x, y, z > 0, chứng minh rằng (x² + y² + z²)/3 ≥ (xy + yz + zx)/3.
Lời giải: Áp dụng bất đẳng thức Cauchy cho bộ ba số, ta có:
(x² + y² + z²)(1 + 1 + 1) ≥ (x + y + z)²
Từ đó rút gọn, chứng minh được điều cần chỉ ra.
Bất đẳng thức Côsi là một kiến thức nền tảng, nhưng lại vô cùng hữu ích trong học tập cũng như nghiên cứu toán học. Việc nắm vững định nghĩa, công thức và cách áp dụng sẽ giúp bạn không còn e ngại với các bài toán chứng minh hay tối ưu. Quan trọng hơn, thông qua quá trình luyện tập, bạn còn rèn luyện được tư duy logic, sự kiên nhẫn và khả năng phân tích vấn đề.