Diện tích xung quanh hình hộp chữ nhật
Trong hình học, hình hộp chữ nhật là một trong những khối hình cơ bản và quen thuộc nhất. Hình hộp chữ nhật xuất hiện ở khắp nơi trong đời sống, từ chiếc hộp quà, viên gạch, đến các thùng hàng. Chính vì vậy, việc nắm được cách tính diện tích xung quanh hình hộp chữ nhật là kiến thức quan trọng không chỉ để làm bài tập toán mà còn để áp dụng vào thực tế.
Diện tích xung quanh của hình hộp chữ nhật chính là tổng diện tích bốn mặt bên, không tính diện tích hai đáy. Đây là đại lượng thường được sử dụng để tính toán khi ta cần bao bọc, dán giấy, sơn hoặc trang trí xung quanh một hình khối mà không quan tâm đến mặt trên và mặt dưới.
Ví dụ đơn giản, khi bạn muốn dán giấy trang trí quanh một chiếc hộp chữ nhật nhưng không dán phần nắp và đáy, điều bạn cần tính chính là diện tích xung quanh.
Hình hộp chữ nhật trong thực tế
Ngoài bài toán học tập, kiến thức này còn được ứng dụng trong nhiều tình huống thực tế. Chẳng hạn, trong ngành xây dựng, diện tích xung quanh hình hộp chữ nhật được dùng để tính lượng sơn hoặc vật liệu cần thiết. Trong thiết kế bao bì, công thức này giúp xác định kích thước giấy bọc. Nhờ đó, bạn thấy rõ rằng học hình học không chỉ phục vụ thi cử mà còn gắn liền với đời sống hàng ngày.
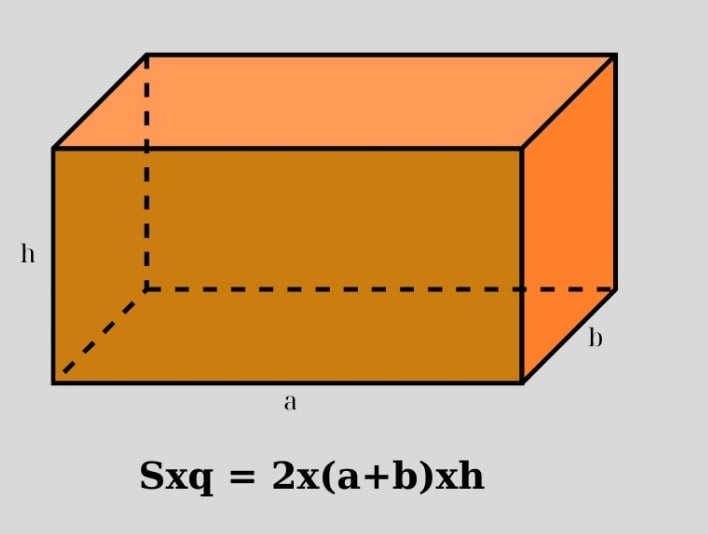
Công thức tính diện tích xung quanh hình hộp
Để tính diện tích xung quanh, ta cần nhớ rằng hình hộp chữ nhật có ba kích thước: chiều dài, chiều rộng và chiều cao. Ký hiệu lần lượt là a, b và h.
Công thức cơ bản
Diện tích xung quanh hình hộp chữ nhật được tính bằng công thức:
Sxq=2h(a + b)
Trong đó:
a là chiều dài
b là chiều rộng
h là chiều cao
Công thức này xuất phát từ việc cộng diện tích bốn mặt bên. Mỗi cặp mặt bên đối diện có diện tích bằng nhau. Hai mặt bên có diện tích a × h, và hai mặt bên còn lại có diện tích b × h. Tổng cộng ta có: 2ah+2bh=2h(a + b).
Phân tích công thức
Điều quan trọng khi học công thức là không chỉ nhớ máy móc mà còn hiểu được nguồn gốc. Khi bạn hiểu rằng diện tích xung quanh chính là tổng của 4 hình chữ nhật ghép lại, bạn sẽ dễ dàng nhớ công thức hơn. Đây cũng là cách giúp bạn tránh nhầm lẫn giữa diện tích xung quanh và diện tích toàn phần.
Công thức mở rộng
Ngoài diện tích xung quanh, bạn cũng cần biết diện tích toàn phần của hình hộp chữ nhật:
Stp=2(ab + ah + bh)
Trong đó Stp là diện tích toàn phần, bao gồm cả hai đáy. Việc phân biệt rõ hai công thức này sẽ giúp bạn không bị lẫn lộn khi làm bài.
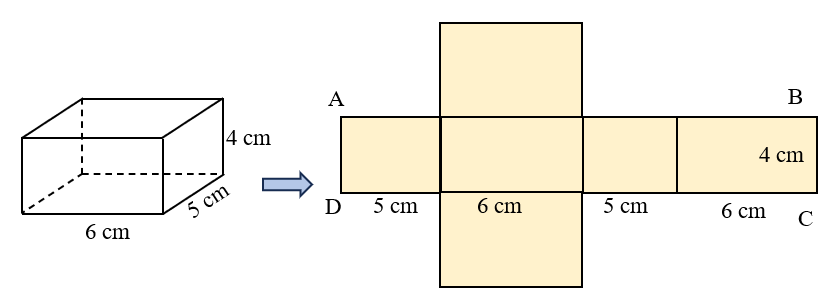
Minh họa bài toán tính diện tích xung quanh
Để hiểu rõ hơn, hãy cùng xem một số ví dụ cụ thể.
Ví dụ 1:
Cho hình hộp chữ nhật có chiều dài a=5 cm, chiều rộng b=3 cm và chiều cao h=7 cm. Tính diện tích xung quanh.
Lời giải:
Sxq=2h(a + b)=2 × 7 × (5 + 3)=14 × 8=112 cm²
Vậy diện tích xung quanh hình hộp chữ nhật là 112 cm² .
Ví dụ 2:
Một thùng hàng có dạng hình hộp chữ nhật, dài 60 cm, rộng 40 cm, cao 50 cm. Người ta muốn dán giấy xung quanh thùng hàng, không dán phần đáy và nắp. Tính diện tích giấy cần dùng.
Lời giải:
Sxq=2h(a + b)=2 × 50 × (60 + 40)=100 × 100=10.000 cm² =1 m²
Như vậy, cần 1 mét vuông giấy để dán xung quanh thùng hàng.
Ví dụ 3:
Một bể nước dạng hình hộp chữ nhật có chiều dài 2 m, chiều rộng 1, 5 m, chiều cao 1, 2 m. Người ta muốn sơn mặt ngoài xung quanh bể, không sơn phần đáy và nắp. Diện tích sơn cần dùng là bao nhiêu?
Lời giải:
Sxq=2h(a + b)=2 × 1, 2 × (2 + 1, 5)=2, 4 × 3, 5=8, 4 m²
Kết quả: diện tích cần sơn là 8, 4 m² .

Tính toán trong bài toán bọc giấy và sơn bể nước
Khi áp dụng công thức, bạn cần chú ý đến đơn vị đo. Nếu các kích thước cho theo cm, kết quả diện tích sẽ tính bằng cm² . Nếu các kích thước tính bằng m, kết quả sẽ là m² . Việc quên đổi đơn vị là lỗi thường gặp nhất khi làm bài tập.
Một điểm dễ gây nhầm lẫn khác là phân biệt diện tích xung quanh và diện tích toàn phần. Nhiều bạn học sinh khi vội vàng thường lấy công thức của toàn phần thay cho xung quanh, dẫn đến kết quả sai. Hãy nhớ: diện tích xung quanh chỉ tính bốn mặt bên, không tính hai đáy.
Ngoài ra, trong một số bài toán thực tế, bạn cần linh hoạt vận dụng công thức. Chẳng hạn, nếu đề yêu cầu tính diện tích giấy bọc quanh hộp nhưng không bọc phần nắp, khi đó bạn chỉ cần lấy diện tích xung quanh rồi trừ đi diện tích một mặt đáy. Sự linh hoạt này giúp bạn giải được nhiều dạng toán khác nhau.
Qua bài viết, bạn đã hiểu rõ khái niệm và công thức tính diện tích xung quanh của hình hộp chữ nhật. Đây là kiến thức quan trọng trong chương trình hình học lớp 5 và lớp 8, đồng thời có ý nghĩa thực tế trong nhiều lĩnh vực đời sống. Khi học công thức, hãy ghi nhớ bản chất của nó xuất phát từ tổng diện tích 4 mặt bên, từ đó bạn sẽ không còn nhầm lẫn.
Việc luyện tập nhiều ví dụ sẽ giúp bạn thành thạo và tự tin hơn khi làm bài kiểm tra cũng như khi ứng dụng vào các bài toán thực tế.
Trên đây là một số thông tin về chủ đề diện tích xung quanh hình hộp chữ nhật. Hi vọng qua bài viết của chúng tôi các bạn đã có cho mình thông tin hữu ích.