Chu vi hình tròn lớp 5
Để giúp học sinh lớp 5 nắm chắc kiến thức, khái niệm chu vi hình tròn có thể được trình bày thành nhiều ý nhỏ rõ ràng như sau:
1. Chu vi hình tròn là gì?
Chu vi là độ dài đường bao quanh một hình tròn.
Có thể hình dung, nếu ta lấy một sợi dây quấn quanh miệng một chiếc bát tròn, sau đó duỗi thẳng sợi dây ra thì độ dài đó chính là chu vi.
2. Ý nghĩa của chu vi hình tròn trong Toán lớp 5
Giúp học sinh hiểu được đặc điểm cơ bản của hình tròn, không chỉ nhìn thấy bằng mắt mà còn đo lường chính xác bằng con số.
Là kiến thức nền tảng quan trọng để học sinh bước sang các bài toán phức tạp hơn như tính diện tích hình tròn, tính độ dài cung tròn hoặc áp dụng trong hình học thực tế.
3. Cách hiểu công thức chu vi hình tròn
Công thức được xây dựng dựa trên mối quan hệ giữa chu vi và đường kính, hoặc giữa chu vi và bán kính.
Dù cách viết khác nhau, bản chất vẫn giống nhau: chu vi là một số lần của đường kính hoặc bán kính, nhân với số gần bằng ba phẩy mười bốn.
Hai cách diễn đạt quen thuộc cho học sinh lớp 5:
Chu vi bằng đường kính nhân với ba phẩy mười bốn.
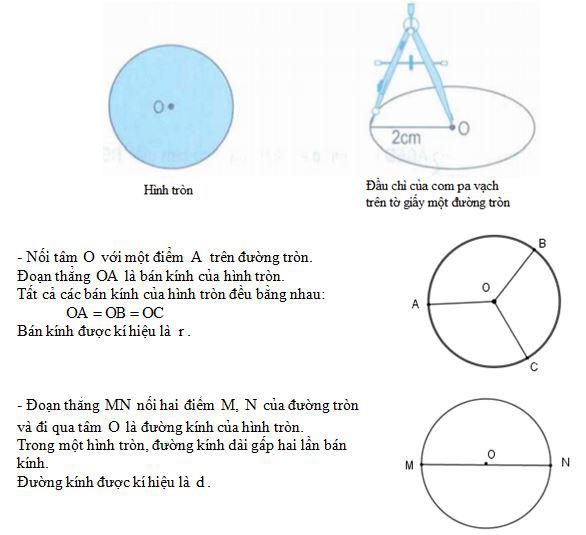
Phân tích chu vi đường tròn
Chu vi bằng hai lần bán kính nhân với ba phẩy mười bốn.
4. Liên hệ thực tế giúp dễ hiểu hơn
Hãy tưởng tượng chiếc bánh xe: nếu bánh xe lăn được một vòng, quãng đường nó đi chính là chu vi của bánh xe đó.
Hoặc chiếc nắp nồi tròn, khi đo độ dài miệng nồi, ta cũng đang đo chu vi của một hình tròn.
Nhờ những ví dụ đời thường, học sinh có thể thấy rằng chu vi hình tròn không phải là kiến thức xa lạ, mà gắn liền với những đồ vật quanh mình.
Công thức
Để học sinh lớp 5 không chỉ nhớ công thức mà còn biết áp dụng thành thạo vào từng dạng bài, phần này có thể được trình bày chi tiết hơn, chia thành nhiều ý nhỏ rõ ràng như sau:
1. Ghi nhớ công thức tính chu vi
Chu vi hình tròn được tính dựa vào mối quan hệ giữa chu vi và đường kính, hoặc giữa chu vi và bán kính.
Có hai cách viết công thức quen thuộc:
Chu vi=Đường kính × 3, 14
Chu vi=2 × Bán kính × 3, 14
Cả hai công thức đều đúng vì đường kính luôn gấp đôi bán kính. Tùy dữ kiện bài toán, học sinh chọn công thức phù hợp để tính toán nhanh hơn.
2. Các bước áp dụng công thức trong từng bài toán
Bước 1: Đọc kỹ đề để xác định xem dữ kiện đã cho là bán kính hay đường kính.
Bước 2: Viết ra công thức tương ứng.
Bước 3: Thay số cụ thể của đề bài vào công thức.
Bước 4: Thực hiện phép nhân cẩn thận, tránh nhầm lẫn.
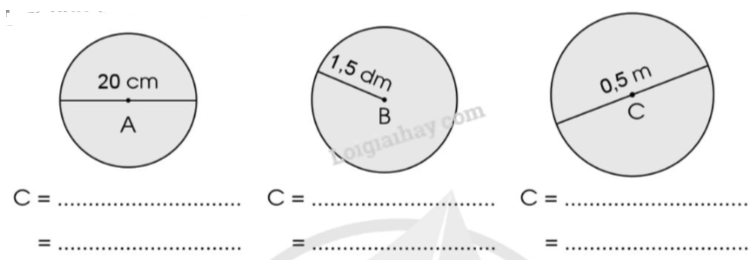
Bài tập
Bước 5: Ghi kết quả cuối cùng kèm theo đơn vị đo (cm, m, km...).
3. Lưu ý quan trọng khi tính chu vi
Luôn chú ý đến đơn vị đo. Nếu bán kính cho bằng mét nhưng đường kính lại bằng cm thì cần đổi về cùng một đơn vị trước khi thay vào công thức.
Không nhầm lẫn giữa bán kính và đường kính. Nếu đề cho bán kính mà áp dụng công thức của đường kính ngay sẽ dẫn tới sai kết quả.
Khi nhân với 3, 14, nên đặt tính cẩn thận hoặc sử dụng máy tính bỏ túi để đảm bảo chính xác.
Trong một số bài, yêu cầu có thể là làm tròn đến một chữ số thập phân. Học sinh cần biết cách làm tròn đúng quy tắc.
4. Sai lầm thường gặp và cách khắc phục
Sai lầm 1: Quên nhân 2 khi áp dụng công thức với bán kính. → Cách khắc phục: luôn nhớ “ bán kính cần nhân đôi để ra đường kính” .
Sai lầm 2: Viết kết quả nhưng bỏ quên đơn vị. → Cách khắc phục: sau khi làm xong, kiểm tra lại và thêm đơn vị vào đáp số.
Sai lầm 3: Nhầm lẫn khi đổi đơn vị, ví dụ từ mét sang cm. → Cách khắc phục: ghi ra bước đổi đơn vị rõ ràng trước khi thay vào công thức.
5. Ví dụ minh họa chi tiết
Ví dụ 1: Hình tròn có bán kính 5 cm.
Chu vi=2 × 5 × 3, 14=31, 4 cm.
Ví dụ 2: Hình tròn có đường kính 12 cm.
Chu vi=12 × 3, 14=37, 68 cm.
Ví dụ 3: Hình tròn có bán kính 1, 5 m.
Chu vi=2 × 1, 5 × 3, 14=9, 42 m.
Qua các ví dụ trên, học sinh thấy rõ rằng việc chọn công thức đúng và thay số chính xác sẽ cho kết quả nhanh chóng và dễ hiểu.
Kiến thức về chu vi hình tròn không chỉ xuất hiện trong sách vở mà còn gắn bó rất chặt chẽ với đời sống hằng ngày. Khi học sinh hiểu rõ và biết áp dụng, các em sẽ nhận ra rằng toán học luôn gần gũi và hữu ích. Có thể chia các ứng dụng thành nhiều ý như sau:
1. Trong việc đo lường các đồ vật tròn
Khi muốn biết độ dài miệng của chiếc bát, chiếc nồi, hay nắp vung tròn, ta thực chất đang đo chu vi hình tròn.
Người thợ thủ công hay người bán hàng có thể cần đo chu vi để làm viền mép, khâu nắp hoặc bọc vải quanh một vật tròn.
2. Trong giao thông và cơ khí
Chu vi của bánh xe chính là quãng đường bánh xe đi được sau một vòng quay.
Biết chu vi bánh xe giúp ta tính toán số vòng quay cần có để di chuyển một quãng đường nhất định.
Ứng dụng này được dùng trong chế tạo xe đạp, xe máy, ô tô và cả trong máy móc có bánh răng tròn.
3. Trong xây dựng và kiến trúc
Khi thiết kế giếng nước, bồn chứa hoặc cột tròn, người thợ cần biết chu vi để ốp gạch, xây tường bao hoặc làm khung.
Ví dụ: xây một bồn nước tròn có đường kính 2 mét, cần biết chu vi để tính toán số viên gạch ốp xung quanh.
4. Trong thể thao và vui chơi
Sân vận động có đường chạy hình tròn hoặc gần tròn, người ta cần biết chu vi để tính số vòng chạy tương ứng với một cự ly.
Trong trò chơi có vòng tròn (ví dụ vòng quay trò chơi, vòng ném), việc hiểu chu vi giúp thiết kế và sử dụng chính xác.
5. Trong đời sống hằng ngày
Khi làm bánh tròn, thợ làm bánh cần biết chu vi để cắt dây hoặc giấy bọc quanh chiếc bánh.
Người may vá hoặc làm thủ công mỹ nghệ dùng chu vi để tính chiều dài vải, ren hoặc dây cần dùng quanh một vật tròn.
Nông dân khi rào quanh một luống cây trồng hình tròn cũng phải đo chu vi để cắt lưới hoặc hàng rào cho vừa.
6. Ý nghĩa của việc học ứng dụng
Giúp học sinh hiểu rằng toán học không chỉ là con số trừu tượng mà còn phục vụ cho mọi lĩnh vực trong đời sống.
Việc liên hệ thực tế làm cho bài học trở nên thú vị, dễ nhớ và dễ vận dụng về sau.