Chu vi hình tròn lớp 5
Trong môn Toán học lớp 5, chu vi hình tròn là một khái niệm cơ bản mà học sinh cần nắm vững. Chu vi của hình tròn là độ dài của đường viền xung quanh hình tròn. Hình tròn là một trong những hình cơ bản trong hình học, với đặc điểm là tất cả các điểm trên đường tròn đều cách đều từ trung tâm. Việc hiểu chu vi hình tròn giúp học sinh giải quyết được nhiều bài toán về hình học, từ việc tính toán diện tích, đến việc đo đạc các vật thể tròn trong thực tế.
Để tính được chu vi hình tròn, chúng ta cần hiểu mối quan hệ giữa bán kính ($r$) (khoảng cách từ tâm đến mép của hình tròn) và đường kính ($d$) (đoạn thẳng nối hai điểm trên đường tròn đi qua tâm). Dưới đây, chúng ta sẽ cùng tìm hiểu công thức tính chu vi hình tròn và ứng dụng của nó trong toán học.
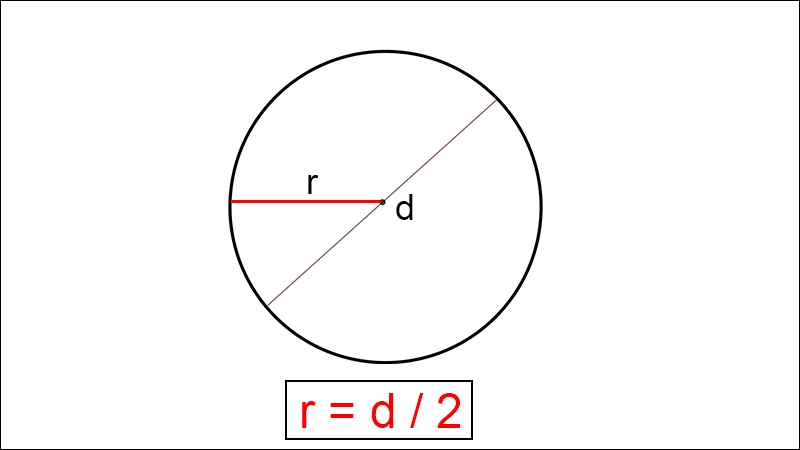
Hình tròn với bán kính và đường kính
Khi bạn muốn tính chu vi của một hình tròn, công thức bạn cần sử dụng là:
C = 2 x π x r
Trong đó, C là chu vi của hình tròn, r là bán kính, và π (pi) là hằng số toán học có giá trị xấp xỉ 3.14. Tuy nhiên, trong một số trường hợp cần độ chính xác cao, người ta có thể sử dụng giá trị chính xác hơn của π, chẳng hạn 3.14159.
Sử dụng Đường Kính
Ngoài ra, nếu bạn biết đường kính của hình tròn (d), công thức tính chu vi sẽ được viết lại như sau:
C = π x d
Trong đó d là đường kính, và bạn sẽ thấy rằng d = 2r, nghĩa là đường kính bằng hai lần bán kính. Công thức này sẽ giúp bạn tính chu vi hình tròn khi bạn chỉ biết đường kính mà không cần phải tính bán kính trước.
Ví Dụ Cụ Thể
Giả sử bạn có một hình tròn có bán kính là 7 cm. Áp dụng công thức C = 2 x 3.14 x 7, ta sẽ tính được chu vi như sau:
C = 2 x 3.14 x 7 = 43.96 cm
Tương tự, nếu bạn biết đường kính của hình tròn là 14 cm, bạn có thể tính chu vi theo công thức C = 3.14 x 14, và kết quả là:
C = 3.14 x 14 = 43.96 cm
Như vậy, dù tính chu vi từ bán kính hay đường kính, kết quả cuối cùng vẫn giống nhau, vì bán kính và đường kính có mối quan hệ trực tiếp với nhau.
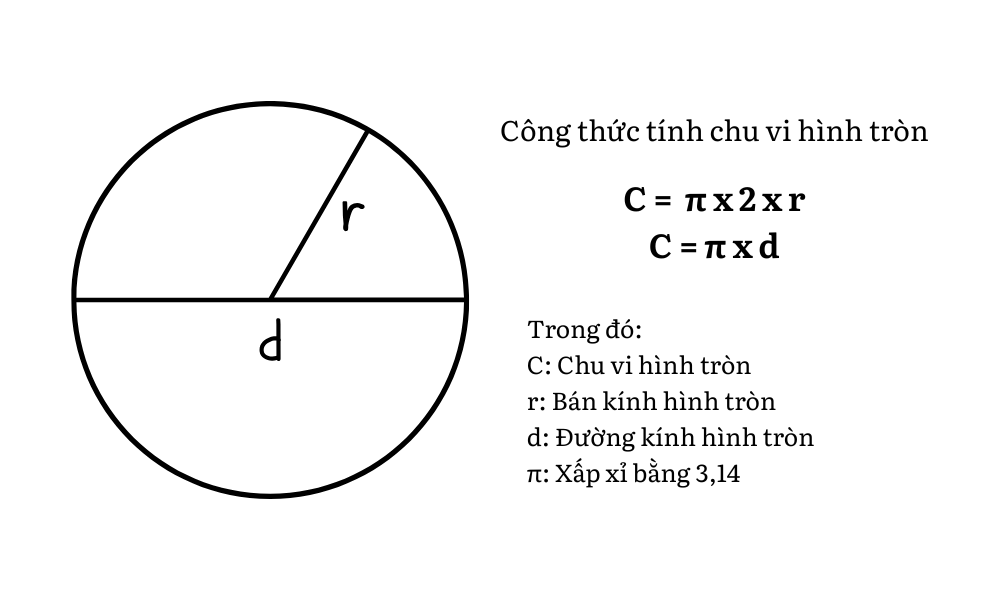
Sử dụng bán kính hoặc đường kính để tính chu vi
>> Xem thêm: 1 tạ bằng bao nhiêu kg
Tính Chu Vi Trong Các Bài Toán Hình Học
Các hằng đẳng thức và công thức về chu vi hình tròn rất quan trọng trong việc giải quyết các bài toán hình học. Khi bạn cần tính diện tích hoặc chu vi của các vật thể hình tròn, công thức này sẽ giúp bạn giải bài toán một cách dễ dàng và nhanh chóng.
Ví dụ, khi tính diện tích của một sân thể thao hình tròn, bạn có thể sử dụng công thức chu vi để tìm ra chiều dài của đường chạy quanh sân, từ đó tính toán các yếu tố liên quan đến quãng đường, số vòng chạy, hoặc lượng vật liệu cần thiết để bao quanh sân.
Tính Chu Vi Trong Các Bài Toán Về Đo Lường
Chu vi hình tròn cũng có ứng dụng trong đời sống hàng ngày, chẳng hạn như khi bạn cần đo chiều dài dây để quấn quanh một hình tròn, hoặc khi cần tính toán lượng sơn hoặc vật liệu cần thiết để bao phủ một vật thể hình tròn như bánh xe, đồng hồ, hoặc các thiết bị tròn khác.
Ví dụ, nếu bạn cần tính chiều dài dây cần dùng để bao quanh một sân chơi tròn có bán kính 50 m, chỉ cần áp dụng công thức chu vi để tính toán.
Ứng Dụng Trong Các Môn Học Khác
Ngoài việc sử dụng trong Toán học, công thức tính chu vi hình tròn cũng có ứng dụng trong các môn học khác như Vật lý và Kỹ thuật. Chẳng hạn, trong các bài toán về chuyển động tròn đều, bạn có thể tính được quãng đường mà một vật thể di chuyển trên quỹ đạo tròn bằng cách sử dụng chu vi hình tròn. Điều này giúp học sinh liên kết lý thuyết trong sách giáo khoa với thực tế.
Ví Dụ 1: Tính Chu Vi Biết Bán Kính
Giả sử bạn có một chiếc bánh pizza hình tròn với bán kính là 10 cm, và bạn muốn biết chiều dài của viền bánh pizza (chu vi). Áp dụng công thức C = 2 x 3.14 x 10, ta có:
C = 2 x 3.14 x 10 = 62.8 cm
Vậy chu vi của chiếc bánh pizza là 62.8 cm. Đây là chiều dài viền của bánh pizza mà bạn có thể sử dụng nếu cần phải bọc hoặc phủ một lớp gì đó lên viền bánh.
Ví Dụ 2: Tính Chu Vi Biết Đường Kính
Nếu bạn có một vòng tròn trang trí với đường kính là 20 cm và cần tính chu vi của nó, bạn chỉ cần áp dụng công thức C = 3.14 x 20:
C = 3.14 x 20 = 62.8 cm
Vậy chu vi của vòng tròn này là 62.8 cm, tương tự như ví dụ trên.
Tính chu vi hình tròn lớp 5 là một kỹ năng cơ bản nhưng vô cùng quan trọng trong môn Toán học. Các công thức tính chu vi, dù là từ bán kính hay đường kính, đều dễ dàng áp dụng và có ứng dụng thực tế rộng rãi trong đời sống hàng ngày. Bằng cách hiểu rõ và thực hành thường xuyên, học sinh có thể áp dụng công thức này để giải quyết các bài toán trong sách giáo khoa cũng như các bài toán thực tế liên quan đến hình tròn.
Việc nắm vững các công thức tính chu vi hình tròn không chỉ giúp học sinh giải quyết các bài tập nhanh chóng mà còn giúp các em phát triển khả năng tư duy toán học và giải quyết vấn đề một cách hiệu quả.
Trên đây là một số thông tin về công thức chu vi hình tròn. Hi vọng với các thông tin chúng tôi cung cấp, các bạn đã có cho mình kiến thức hữu ích. Chúc các bạn học tốt và áp dụng tốt kiến thức về chu vi hình tròn vào các bài toán!