7 hằng đẳng thức lớp 8
7 hằng đẳng thức lớp 8 là kiến thức quan trọng trong chương trình toán học THCS. Kiến thức này, các em sẽ được làm quen khi vào lớp 8. Khi lên các lớp cao hơn thì bảy đẳng thức đáng nhớ này cũng được áp dụng trong các bài toán nâng cao nhiều hơn. Và cũng như theo các bạn suốt quãng đường học tập. Bảy đẳng thức đáng nhớ giống như tên gọi của nó, “đáng nhớ” ở đây ở việc giúp các em tiếp thu kiến thức. Hơn nữa, hằng đẳng thức cũng là công cụ đem lại nhiều lợi ích khi áp dụng vào môn toán ở chương trình học tập.
Vai trò của 7 hằng đẳng thức lớp 8
Khi đã nắm chắc kiến thức và cách dùng, việc vận dụng tốt 7 hằng đẳng thức đáng nhớ để giải toán là điều không khó. Điều này sẽ giúp học sinh tiết kiệm được thời gian, công sức trong việc giải bài tập. Đồng thời đây cũng là cách giải dễ hiểu và hạn chế nhiều sai sót khi biến đổi công thức.
7 hằng đẳng thức lớp 8 là công cụ không thể thiếu trong vốn kiến thức của các em. Nhờ việc học các hằng đẳng thức này sẽ giúp các bạn học sinh rèn được các kỹ năng quan sát, nhận xét. Đồng thời tỉ mỉ hơn trong khi phân tích các vấn đề trong toán học. Cũng như rèn luyện các kỹ năng cẩn thận cả trong những tình huống đời thường.
Khi vận dụng tốt các hằng đẳng thức, kết quả học tập của các em cũng được nâng cao. Các em sẽ thấy thích thú, đam mê và có tinh thần hứng thú trong việc học toán. Hay việc suy nghĩ cách giải bài toán ở những bài tập khó phải áp dụng hằng đẳng thức để phân tích cũng tăng sự tư duy, tăng sự phát triển não bộ. Ngoài ra, các đẳng thức đáng nhớ góp phần trong việc phát triển trí tuệ và rèn luyện sự thông minh của trẻ ngay từ nhỏ.
7 hằng đẳng thức đáng nhớ bao gồm:
1. ( a + b )2 = a2 + 2ab + b2
2. (a - b )2 = a2 - 2ab + b2
3. a2 - b2 = ( a - b )( a + b )
4. ( a + b )3 = a3 + 3a2b + 3ab2 + b3
5. ( a - b )3 = a3 - 3a2b + 3ab2 - b3
6. a3 + b3 = ( a + b )( a2 - ab + b2 )
7. a3 - b3 = ( a - b )( a2 + ab + b2 )
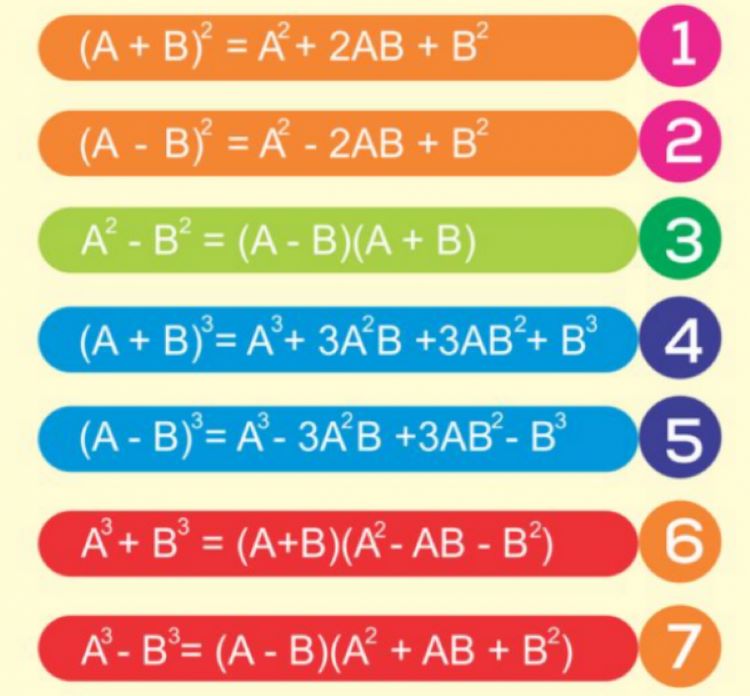
7 Hằng đẳng thức đáng nhớ
1. Bình phương của một tổng
Bình phương một tổng bằng bình phương số thứ nhất cộng với hai lần tích của số thứ nhất với số thứ hai, sau đó cộng với bình phương của số thứ hai.
( a + b )2 = a2 + 2ab + b2
Ví dụ: Khai triển các hằng đẳng thức sau:
a) ( x + 2 )2
b) ( 2x + 1 )2
Giải
a) ( x + 2 )2 = x2 + 2.x.2 + 22 = x2 + 4x + 4
b) ( 2x + 1 )2= ( 2x )2 + 2.2x.1 + 12 = 4x2 + 4x + 1
2. Bình phương một hiệu
Bình phương của một hiệu sẽ bằng bình phương của số thứ nhất trừ đi hai lần tích của số thứ nhất và số thứ hai, sau đó cộng với bình phương của số thứ hai.
( a - b )2 = a2 - 2ab + b2
Tham khảo: Chu vi hình tròn lớp 5

Công thức tính bình phương của một hiệu
Ví dụ: Khai triển các biểu thức sau theo hằng đẳng thức:
a. (2x-3y)2
b. (4y-2)2
Giải:
a. (2x-3y)2 = 4x2-12xy+ 9y2
b. (4y-2)2= 16y2-16y+4
3. Hiệu của hai bình phương
Hiệu của hai bình phương chính bằng tổng của hai số nhân với hiệu của hai số.
a2 - b2 = ( a - b )( a + b )
Ví dụ: Khai triển các biểu thức sau
a) x2 - 16 b) x2 - 4y2
Giải
a) x2 - 16 = x2 - 42 = ( x - 4 )( x + 4 )
b) x2 - 4y2 = x2 - ( 2y )2 = ( x - 2y )( x + 2y )
4. Lập phương của một tổng
Lập phương của một tổng bằng lập phương số thứ nhất cộng với ba lần bình phương của số thứ nhất nhân số thứ hai, đem cộng với ba lần bình phương số thứ hai nhân số thứ nhất sau đó cộng với lập phương của số thứ hai.
( a + b )3= a3 + 3a2b + 3ab2 + b3
Ví dụ: Khai triển biểu thức sau: ( x + 3y )3
Giải
( x + 3y )3 = x3 + 3.x2.3y + 3.x.( 3y )2 + ( 3y )3
= x3 + 9x2y + 18xy2 + 27y3
5. Lập phương của một hiệu
Lập phương của một hiệu bằng lập phương số thứ nhất trừ đi ba lần bình phương số thứ nhất nhân số thứ hai, đem cộng với ba lần bình phương số thứ hai nhân số thứ nhất sau đó trừ đi lập phương của số thứ hai.
( a - b )3 = a3 - 3a2b + 3ab2 - b3

Công thức tính lập phương của một hiệu
Ví dụ: Khai triển biểu thức sau theo hằng đẳng thức: ( 2x - 2y )3
Giải
( 2x - 2y )3 = (2x)3 - 3.(2x)2.2y + 3.2x.( 2y )2 - ( 2y )3
= 8x3 - 24x2y + 24xy2 - 8y3
6. Tổng của hai lập phương
Tổng của hai lập phương sẽ bằng tổng của hai số sau đó đem nhân với bình phương thiếu của hiệu số thứ nhất với số thứ hai.
a3 + b3 = ( a + b )( a2 - ab + b2 )
Ví dụ: Khai triển biểu thức sau theo hằng đẳng thức: x3 + 27
Hướng dẫn:
x3 + 27 = x3 + 33= ( x + 3 )(x2 - x.3 + 32) = ( x + 3 )( x2 - 3x + 9 )
7. Hiệu của hai lập phương
Hiệu của hai lập phương sẽ bằng hiệu số thứ nhất trừ đi số thứ hai sau đó đem nhân với bình phương thiếu của tổng số thứ nhất với số thứ hai.
a3 - b3 = ( a - b )( a2 + ab + b2 )
Ví dụ: Khai triển biểu thức sau: 8x3- 27= (2x-3)(4x2+6x+9)
Khai triển các hằng đẳng thức sau:
a) ( 2x + 3) 2
b) ( 3x - 2 )3
c) ( x + 4 )3
d) 4x2 - 16
e) x3 + 125
f) 27x3 - ⅛ x3
g) x2 - 16y2
h) ( x + 2y)2
i) ( 2x + 3y )2
j) ( x - 2y)2
k) ( 3x - y )3